Optical Tomography
Optical Tomography
Collaboration : Dr. Martin Schweiger and Prof. Simon Alridge , University College, London; Dr. Steve Parker and Prof. Chris Johnson, University of Utah.
 |
 |
Optical Tomography is a method of using light in a narrow wavelength band in the near-infrared part of the spectrum to transilluminate tissue and to use the resulting measurement of intensity on the tissue boundary (both due to transmission and reflection) to reconstruct a map of optical properties within the tissue. Under the assumption, that forward problem is governed by a diffusion equation one can use FEM to find a numerical solution. Then classical optimization algorithms can be used to determine the properties of the media.
One of the tissue parameters which can be obtained by optical tomography is local oxygenation. Primarily applications of this imaging technique is a monitoring of cerebral blood and tissue oxygenation of newborn infants, functional mapping of brain activation during physical or mental exercise and imaging of the breast to detect tumor.
The diffuse scattering of light prohibits the use of such popular topographic reconstruction methods as Radon transforms and leaves iterative inverse model based reconstruction techniques.
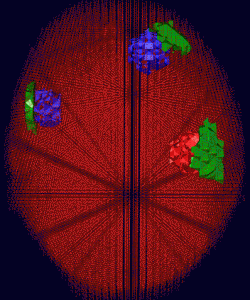
As a test case we consider a head mesh composed of a regular grid of tetrahedra. The mesh is constructed from a segmented 3D MRI data set and scaled to the size of a newborn baby. Available meshing tools allow the generation of meshes of various resolution. We assigned optical properties to the elements similar to those previously reported . Figure shows a simple test case of reconstruction of absorbing and scattering perturbations inside the brain after 40 iterations of a nonlinear conjugate gradient method. The initial guess was the background tissue parameters without the perturbation. Target perturbations where spheres of 5 mm radius embedded in the grey matter region. Two of the objects were absorption perturbations at 3 and 4 times the background value, and one was a scatter perturbation at 8 times the background value.
 |
 |
Martin Schweiger, Leonid Zhukov, Simon R. Alridge and Christopher R. Johnson
Optical tomography using the SCIRun problem solving environment: Preliminary results for three-dimensional geometries and parallel processing. Optics Express (1999)